Ágora dixital
Imagina que estás en una competición en la que tienes que diseñar el tobogán más rápido, con un tiempo de caída menor. Que forma le darías? Sabías que tiene mucho en común con el vuelo de los aviones?
En esta experiencia aprenderás el significado del concepto braquistocrona, al tiempo que trabajas conceptos de cinemática como la velocidad o el tiempo de caída, y valorarás la importancia de la trayectoria en el estudio de los movimientos.

Cesta de materiales
Presiona en los puntos interactivos de la imagen.
Manos a la obra
- Paso 1
-
- Observa los tres tipos de trayectorias posibles para las canicas. ¿En cuál de ellas piensas que tardará menos tiempo en llegar la canica al final?
- Realizad una lluvia de ideas en la clase, de forma ordenada y argumentada.
- Paso 2
-
- Realizad el lanzamiento y grabadlo con un móvil en cámara lenta. Iniciad el cronómetro cuando comience el descenso, y aseguraos de que la pantalla del cronómetro queda grabada en el vídeo. Es importante que las tres canicas inicien el movimiento simultáneamente, por lo que debéis discurrir algún sistema de lanzamiento.
- Paso 3
-
- Comprobad el orden de llegada visualizando el vídeo en cámara lenta y los tiempos de llegada. ¿Cuál llegó primera? ¿Cuál de última? ¿Por qué creéis que pasó esto?
- Realizad una lluvia de ideas en el aula de forma ordenada y argumentada.
- Paso 4
-
- Realizad varios lanzamientos (mínimo 5) y anotad los tiempos en cada repetición. Calculad el tiempo medio de caída (\( t_m \)).
- Paso 5
-
- Mide la distancia entre los puntos inicial y final de las trayectorias (\(\Delta r \)) y calcula velocidad media en cada una. Recuerda que la velocidad media se calcula como: \[v_m=\frac{\Delta r}{t_m}\].
- Paso 6
-
- ¿Sabíais que la cicloide, además de ser la trayectoria que hace que caiga en un tiempo menor (braquistocrona), también tiene la propiedad de que el tiempo de caída es siempre el mismo, independientemente del punto inicial (tautócrona)? Compruébalo lanzando las canicas desde puntos diferentes de la cicloide y anotando los tiempos de caída. (Tiene en cuenta el error experimental).
Vsauce. The Brachistochrone (Dominio público) - Paso 7
-
Comunica los resultados. Redactad en grupo un pequeño informe sobre lo observado y las conclusiones obtenidas. Recordad emplear un lenguaje científico. El informe debe ser breve e incluir los siguientes apartados:
- Introducción y hipótesis: ¿Cuál era el problema? ¿Qué hipótesis propusisteis en la clase?
- Resultados: Recopilad de forma ordenada los tiempos de caída y las velocidades medias calculadas.
- Análisis de los resultados: ¿Qué observasteis? ¿A qué es debido?
- Conclusiones: ¿Qué conclusiones obtuvisteis? ¿Creéis que hay otras situaciones en las que la línea recta no sea la que invierte menos tiempo? Propón algún ejemplo que se te ocurra de la vida cotidiana.
Tips docentes
- Consejos técnicos
-
Los consejos técnicos te servirán para construir la braquistocrona sin problemas, tanto con el alumnado como por ti mismo/la:
1. Se tienes acceso a una cortadora láser:
Puedes emplear los siguientes diseños (descárgalos en formato .svg)
ImaxeCicloide (Dominio público) ImaxeHipérbola (Dominio público) ImaxePlano inclinado (Dominio público) Cicloide Hipérbola Plano Inclinado Puedes emplear otros materiales de los que dispongas, como metacrilato.
2. Si no tienes acceso a una cortadora láser:
Realiza los cortes con una sierra de calar.
Dibuja las trayectorias a mano:
- La hipérbola puedes construirla dibujando unos ejes coordenados y pintando varios puntos. Si te resulta complicado, puedes sustituirla por cualquier otra trayectoria que vaya por debajo de la cicloide (dos planos inclinados de distinta pendiente, una trayectoria "inventada"...).
- Para el caso de la cicloide puedes emplear el siguiente tutorial:
Carlos López Bueno. Tutorial Construcción Cicloide (CC BY-NC-SA)
Puedes emplear otros materiales, como el poliespán. Se empleas este material, es recomendable construir una cortadora de poliespán con hilo de nicrom.
Tecnología con Clase. Cortador Porexpan muy sencillo (Dominio Público) Cuanto mayores sean las dimensiones de las trayectorias, mejor se verá el efecto.
Construye primero la cicloide y adapta las otras curvas a esta. La altura es el diámetro de la circunferencia generatriz (la que nos sirve para construir la cicloide), mientras que la longitud será 𝜋⋅𝑅, siendo R el radio de la circunferencia generatriz. Adapta estos valores al tamaño de tus tablas.
siguiente vídeo puedes ver un ejemplo de cómo debería quedar y funcionar el experimento, lo que te ayudará a comprender cómo construirlo y a visualizar el resultado final.
DrTxux. Curva Braquistocrona FI-UNAM (Dominio público) Puedes construir y montar tu propio sistema de cronometraje para la medida de los tiempos de caída, con un coste reducido. Para esto solo tienes que seguir las siguientes instrucciones:
- Cesta de materiales:
- Conecta los detectores IR en el punto más bajo de las curvas, de manera que las canicas pasen por encima de ellos en el descenso.
- Conecta el pulsador de manera que se suelte automáticamente con el dispositivo que emplees para realizar el lanzamiento simultáneo de las tres canicas (el cronómetro se inicia cuando el pulsador se suelta).
- Conecta estos elementos siguiendo el siguiente esquema de conexiones.
Imaxe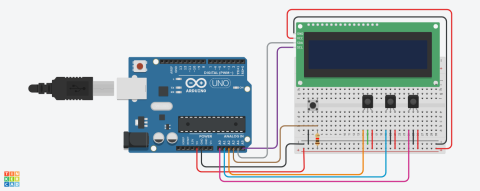
Carlos López Bueno. Esquema de conexiones para la construcción de un cronómetro automático. (CC BY-NC). - Programa el Arduino con el siguiente código de programación. Teniene cuidado de descargar las librerías necesarias.
Explicación general sobre el funcionamiento del cronómetro. Por una parte, tenemos un pulsador con palanca que, cuando se suelta a palanca inicia el cronometraje. Está pensado para que el sistema de retención de las canicas "pise" el pulsador mientras las está reteniendo, y suelte el pulsador automáticamente cuando se sueltan las canicas. Una vez pasa eso, tenemos en realidad tres cronómetros, uno para cada trayectoria. Cada una de ellas tiene un detector IR al final de la trayectoria, de forma que cuando la canica pase por encima de él pare el cronómetro de forma automática. Esto es independiente de que pase con las otras trayectorias, y así al final tendremos medidos los tiempos de las tres trayectorias.
- Orientaciones y variaciones metodológicas
-
Los siguientes puntos soy solo consejos y posibles variaciones que se pueden adaptar mejor a tus preferencias. Puedes realizar todas las modificaciones que consideres oportunas..
Si no cuentas con un sistema de cronometraje automático, es necesario realizar varios lanzamientos para observar el efecto de curva tautócrona. El error experimental probablemente sea grande, y es muy posible que no se observe con pocos lanzamientos. Haciendo varios lanzamientos se observará que el tiempo no está correlacionado con la altura del lanzamiento.
Aunque la definición estricta de velocidad media emplea el desplazamiento y no el espacio recorrido, también es habitual ver esta otra definición. Si prefieres calcularla de este modo también es interesante, e incluso se pueden comparar los resultados calculándolo de ambas maneras.
Resulta interesante realizar un proyecto compartido entre los Departamentos de Física y Química y de Tecnología. En este caso el alumnado podría construir las diferentes trayectorias, aprendiendo a manejar las diferentes herramientas del taller, mientras que en la materia de Física y Química se analizaría el movimiento.
Para la elaboración de informes es recomendable emplear herramientas de edición de texto compartido. De este modo pueden finalizarla en la casa si no son quien de finalizarla en la sesión. Pueden emplear Google Docs, o crearle la cada grupo un documento en Abalarbox.
Es posible variar el número de integrantes del grupo, e incluso realizar la tarea de manera individual.
Tu clase en un clic
Implementa esta microsecuencia en tu aula Moodle (Descarga disponible en gallego o castellano ).
|
Imaxe

|
Imaxe

|



