Ágora dixital
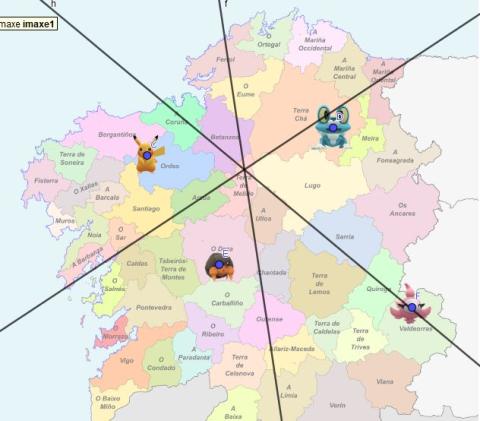
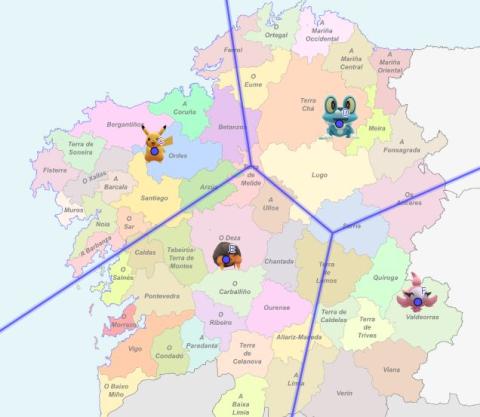
Toda Galicia está en alerta. En las últimas horas se avistaron Pokémons en cuatro comarcas de esta comunidad. Nuestra misión consiste en trazar un plan para organizar los comandos de busca.
La geometría tiene muchas utilidades en el mundo real y son importantes en la vida de muchas personas.
En esta microsecuencia vamos a descubrir los diagramas de Voronoi. Con ellos, podemos dividir un plano que contenga una determinada cantidad de puntos fijo en la misma cantidad de regiones que contienen los puntos del plano que minimizan las distancias a los puntos de partida.
Esta manera de dividir un plano permite, por ejemplo, evitar colisiones de barcos o conocer sobre el campo de fútbol cuál es el equipo dominante. También sirve para dividir una ciudad en áreas, cuando se pretende minimizar el recorrido a determinados puntos como pueden ser farmacias, colegios u otros puntos de interés. Puedes ver ejemplos gráficos en este enlace1.
En el mundo de la medicina, se descubrió recientemente en Sevilla un método de detección de cáncer tras observar que los tejidos epiteliales siguen un modelo geométrico que se desarrolla a partir de diagramas de Voronoi.
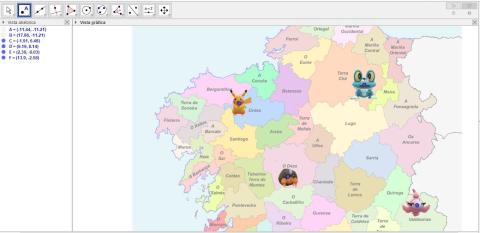
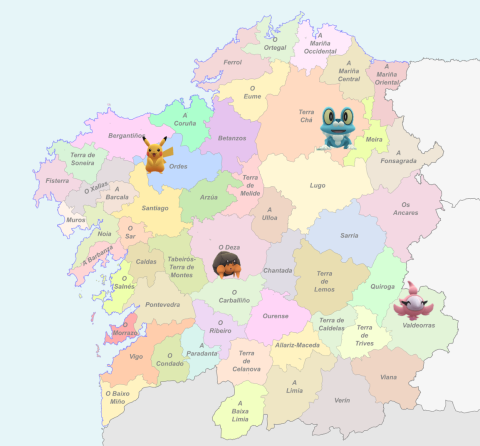
Siguiendo este modelo, vamos a dividir el territorio gallego en cuatro áreas. La búesqueda de cada Pokémon la van a hacer las personas que están más cerca de él, que de los otros tres.
Cesta de materiales
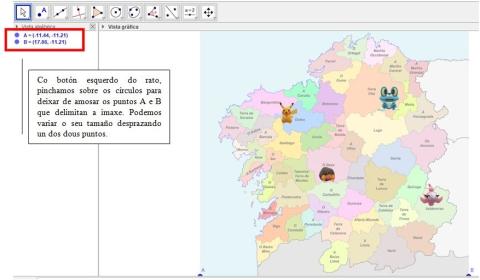
Presiona en los puntos interactivos de la imagen.
Manos a la obra
- Paso 1
-
- Preparamos la aplicación Geogebra:
- Si lo has instalado en tu ordenador, abre la aplicación Geogebra Classic (en portátiles E-Dixgal: menú Aplicaciones → Educación → Geogebra Classic). En caso contrario, presiona en este enlace2 (No precisa registro).
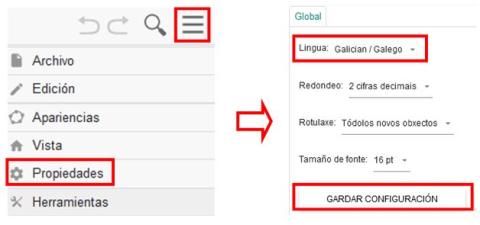
- Presiona en el menú de la parte superior derecha de la aplicación → Propiedades → Lengua: Spanish/Español → Guardar configuración.
ImaxeCaptura de pantalla de Geogebra - En la vista gráfica, eliminamos ejes y cuadrícula (desde el menú de la barra de la parte superior o presionando con el botón derecho sobre la pantalla gráfica).
- Preparamos la aplicación Geogebra:
- Paso 2
-
- Importamos la imagen de fondo
- Descarga en tu ordenador a imagen de este enlace3.
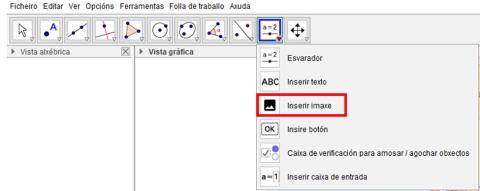
- Para insertar imágenes en Geogebra, debes seguir los pasos de la siguiente captura de pantalla.
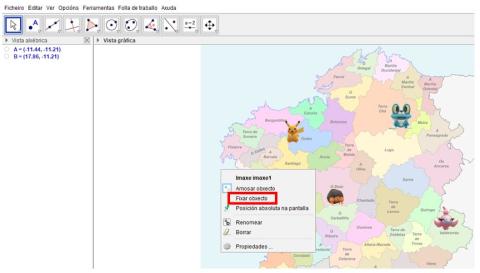
ImaxeCaptura de pantalla de Geogebra ImaxeCaptura de pantalla de Geogebra - Con el botón derecho del ratón sobre la imagen, se abre un menú. Elegimos “Fijar objeto”.
ImaxeCaptura de pantalla de Geogebra - Importamos la imagen de fondo
- Paso 3
-
Mediatrices y circuncentro en un triángulo.
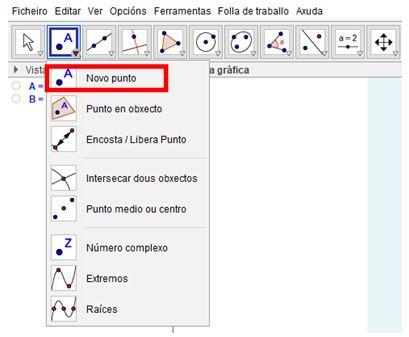
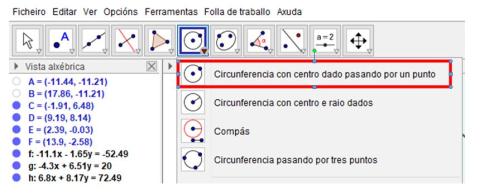
- Con la herramienta “Nuevo punto”
ImaxeCaptura de pantalla de Geogebra - Marca un punto en el centro de cada uno de los Pokémons de la imagen, siguiendo esta orden en las comarcas:
- Ordes (punto C)
- Terra Chá (punto D)
- O Deza (punto E)
- Valdeorras (punto F)
- En los siguientes apartados, planificaremos la busca en las tres primeras comarcas. Hasta que no veamos que el plan funciona, no tendremos en cuenta el Pokémon que se avistó en la comarca de Valdeorras o incluso posibles avistamientos futuros.
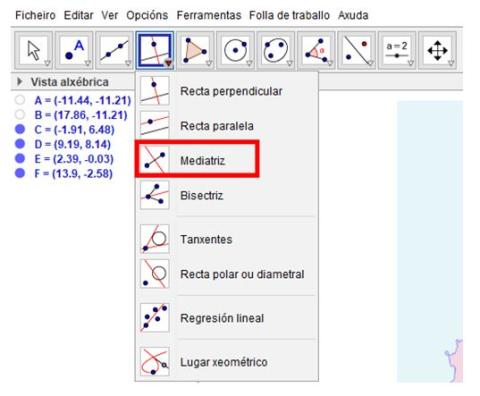
ImaxeCaptura de pantalla de Geogebra - Con la herramienta “Mediatriz”
ImaxeCaptura de pantalla de Geogebra - Marca por parejas los puntos
- C y D
- C y E
- D y E
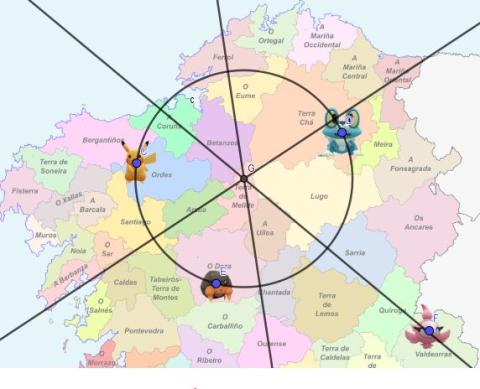
- Si todo fue bien hasta ahora, en tu pantalla debes estar en este punto:
ImaxeCaptura de pantalla de Geogebra - Análisis de resultados. Si consideramos el triángulo de vértices CDE:
- Las tres mediatrices tienen un punto en común. ¿Cómo se llama ese punto?
- La explicación de que se llame así puedes verla con la herramienta.
- Paso 4
-
Mediatrices y circuncentro en un triángulo
- Con la herramienta “Nuevo punto”
ImaxeCaptura de pantalla de Geogebra marca un punto en el centro de cada uno de los Pokémons de la imagen, siguiendo esta orden en las comarcas:
- Ordes (punto C)
- Terra Chá (punto D)
- O Deza (punto E)
- Valdeorras (punto F)
En los siguientes apartados, planificaremos la busca en las tres primeras comarcas. Hasta que no veamos que el plan funciona, no tendremos en cuenta el Pokémon que se avistó en la comarca de Valdeorras o mismo posibles avistamientos futuros.
ImaxeCaptura de Pantalla de Geogebra Con la herramienta “Mediatriz”
ImaxeCaptura de pantalla de Geogebra Marca por parejas los puntos:
- C y D
- C y E
- D y E
Si todo fue bien hasta ahora, en tu pantalla debes estar en este punto:
ImaxeCaptura de pantalla de Geogebra - Análisis de resultados. Si consideramos el triángulo de vértices CDE:
- Las tres mediatrices tienen un punto en común. ¿Cómo se llama ese punto?
- La explicación de que se llame así puedes verla con la herramienta:
ImaxeCaptura de pantalla de Geogebra - Salta con el ratón primero en el punto de corte de las mediatrices y después en uno de los tres puntos C, D o Y. No debería de sorprenderte este resultado:
ImaxeCaptura de pantalla de Geogebra - Paso 5
-
Diagramas de Voronoi
- Igual que ocultabas los puntos A y B en el apartado 2.1, ahora debes ocultar las tres mediatrices y la circunferencia. (¡Ojo! no se trata de eliminar, solo se dejan de ver en la vista gráfica). El aspecto en la vista gráfica ha de ser el mismo que el de la imagen del apartado 3.1.
- Comenzamos por hacer el diagrama de Voronoi, teniendo en cuenta en el mapa solo los puntos C, D y E. Para eso, en la barra de comandos de la parte algébrica escribimos:
grafo1=Voronoi(C,D,Y)
(Observa que no hay ningún espacio entre los caracteres del comando).
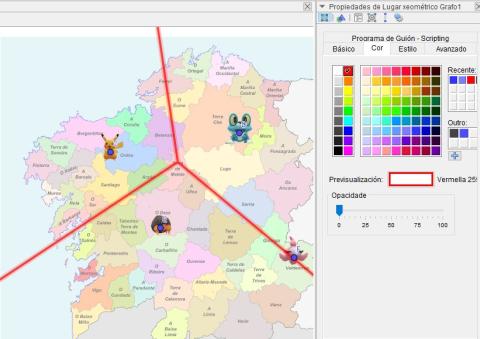
- Con el botón derecho sobre alguno de los segmentos que forman el diagrama, ve a las Propiedades del mismo. En las pestañas Color y Estilo, cámbiale el color y el grosor. El resultado debería ser similar a este:
Imaxe- Relación del diagrama de Voronoi con las mediatrices.
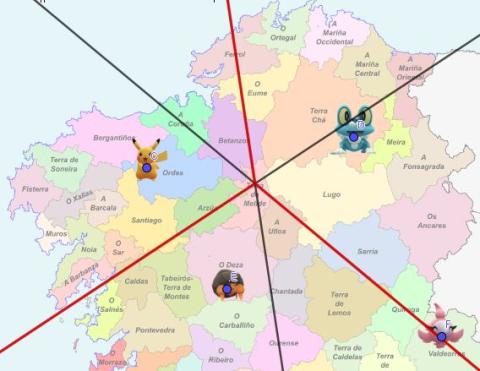
Ahora volverás a mostrar las tres mediatrices que ocultabas en el apartado 4.1. Puede que te sorprenda comprobar que el diagrama de Voronoi está trazado con semirrectas de las mediatrices dibujadas anteriormente. Además, el circuncentro es lo que determina el punto extremo de cada una de ellas.
ImaxeCaptura de pantalla de Geogebra Teniendo en cuenta el concepto de mediatriz, ¿qué crees que se puede concluir de esta coincidencia? ¿Tenemos una buena solución para repartir el territorio de forma eficiente?
- Fin de la misión
Conseguimos una buena solución para repartir el territorio gallego, de forma que los comandos de busca de Pokémons de cada zona, solo tendrán que acercarse a aquel que se encuentra a la menor distancia posible.
Volvemos a ocultar todas las mediatrices y el diagrama de Voronoi anterior y escribimos en la línea de órdenes de la Vista algébrica:
Grafo2=Voronoi(C,D,E,F)
El plan de actuación queda reflejado gráficamente de este modo:
ImaxeCaptura de pantalla de Geogebra
Tips docentes
Los tips del profesorado son pequeñas ayudas para desarrollar la estrategia educativa de forma adecuada.
La versión online de Geogebra permite su uso sin necesidad de registrarse. Los trabajos no quedarán guardados, pero se pueden descargar con la extensión .ggb
Esta práctica está pensada para el nivel de 1º ESO, puesto que en el bloque de Geometría, se trabajan los puntos y rectas notables de los triángulos.
Otro experimento con el cual se puede dividir un plano mediante diagramas de Voronoi, consiste en emplear dos placas transparentes y pintura acrílica de distintos colores, procediendo cómo se ve en la siguiente secuencia de imágenes:
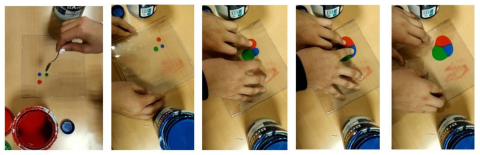
Esta microsecuencia se puede aprovechar para hacer alguna actividad interdisciplinar con materias como Lengua Gallega o Geografía y Historia.
Tu clase en un clic
Implementa esta microsecuencia en tu aula Moodle (Descarga disponible en gallego o castellano ).
|
Imaxe
 |
Imaxe
 |