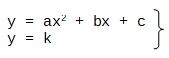¿A quién no le gustaría diseñar su propia tipografía?

Imaxe

Comenzaremos por la letra A. Aprenderás a diseñar paso a paso las letras del abecedario, empleando gráficas de funciones. Verás que es muy sencillo.

Podrás seguir haciendo nuevas letras. Así, con un poco de imaginación, podrás diseñar una línea propia de productos para lucir tu tipografía.

Cesta de materiales

Presiona en los puntos interactivos de la imagen.

Manos a la obra

Paso 1

• Esbozo de la letra A.
• En tu libreta, representa unos ejes cartesianos. Haz un esbozo de una letra A. Esta vez la haremos con un trozo de parábola y un trozo de recta que corte la parábola horizontalmente. (Aconsejamos que la parábola tenga su vértice en la parte positiva del eje Y y que los extremos sean puntos del eje X).

 

 Paso 2

• Ecuación de la parábola:

Para determinar la ecuación de una parábola necesitamos conocer tres puntos de sus coordenadas.

• Sobre la parábola, marca el vértice y los puntos de corte con los ejes. (Aconsejamos que todos tengan coordenadas enteras).
• Para cada uno de los tres puntos, sustituye sus respectivas coordenadas en la ecuación de una función cuadrática:
• Resuelve el sistema de ecuaciones resultante, y así obtendrás los valores de los parámetros a, b y c, y tendrás la ecuación de tu parábola.

y= ax² bx c

Paso 3

• Esta es más sencilla. Recuerda que las rectas horizontales son las gráficas de las funciones constantes:

y = k

Paso 4

• Restricciones:

   

  • Geogebra nos permite representar trozos de funciones, introduciendo un condicional para representar una parte de la gráfica en un intervalo determinado.
  • El trozo de parábola está restringido al intervalo [-m, m], siendo (-m, 0) y (m, 0) los puntos de corte de la parábola con el eje X.
  • El trozo de recta estará definido en el intervalo comprendido entre los puntos en que se corta con la parábola. Para calcularlos, debes resolver el sistema formado por las respectivas ecuaciones:

Imaxe

 

•  La recta quedará restringida al intervalo [-n, n], siendo (-n, k) y (n, k) los puntos de corte de la parábola con la recta.

 

Paso 5

En tu libreta haz un resumen del proceso, anotando en una tabla las funciones con las respectivas restricciones. (Deberás sustituir los parámetros a, b, c, k, m y n por los valores obtenidos en los cálculos).

 

Imaxe

 

Paso 6

Representación en Geogebra:

• 6.1. Si lo has instalado en tu ordenador, abre la aplicación Geogebra Classic (en portátiles E-Dixgal: menú Aplicaciones → Educación → Geogebra Classic).

En caso contrario, presiona en este enlace (No precisa registro).

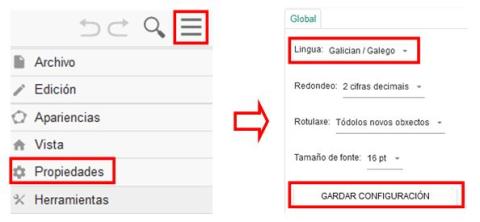
• 6.2. Presiona en el menú de la parte superior derecha de la aplicación en "Propiedades", en "Lengua: Spanish/Español"  y después en "Guardar configuración".

Imaxe

• 6.3. Y en las dos líneas de comando, escribe los textos en letra gruesa del cuadro siguiente, cambiando los parámetros a, b, c, k, m y n por los valores que tienes recogidos en la tabla:

	Línea 1: Si(-m≤x≤m,ax2 bx c) Línea 2: Si(-n≤x≤n,k)

 

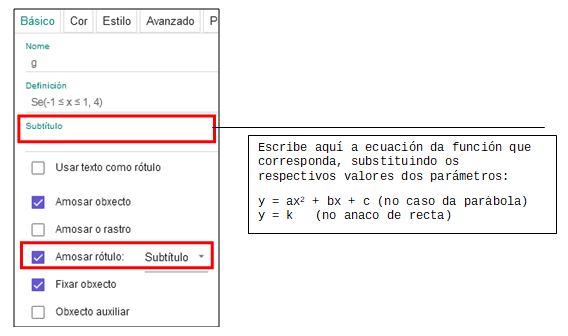
• 6.4. Si consigues visualizar tu letra A, ya solo tienes que darle formato, situándote sobre cada trozo de gráfica (Botón derecho -Configuración) en la pestaña "Básico" cambia el rótulo como se muestra en el gráfico. Cambia también el color y el grosor de las líneas.

Imaxe

 

Paso 7

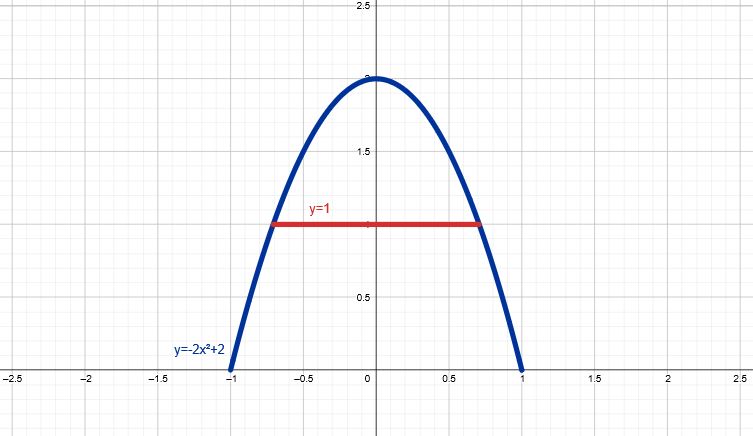
• Resultado: Llegado a este punto, ya deberías estar visualizando tu letra A. ¡Enhorabuena si lo has logrado!

Imaxe

Tips docentes

Los tips del profesorado son pequeñas ayudas para desarrollar la estrategia educativa de forma adecuada.

 La versión online de Geogebra permite su uso sin necesidad de registrarse. Los trabajos no quedarán guardados, pero se pueden descargar con la extensión .ggb.

 Esta práctica está pensada para cursos superiores de la etapa de la ESO. En 4º será posible introducir otras funciones más complejas, como la raíz cuadrada, exponenciales, logarítmicas e incluso las trigonométricas. Se pueden trabajar también las transformaciones de funciones: traslaciones, simetrías o deformaciones.

 La microsecuencia se puede adaptar para 2º ESO, puesto que solo con rectas ya es posible hacer buena parte del abecedario.

 En Geogebra, cuando se precise representar rectas verticales, habrá que emplear la herramienta:

Imaxe

 En el paso 6.2 es muy importante que el alumnado haya definido el idioma, para que Geogebra reconozca el condicional. En caso contrario, dará error o simplemente no va a reconocer el comando. De estar configurado en inglés, debería emplearse como If(), de estarlo en gallego, el comando sería Se()

 En el punto 6.3, se puede proponer al alumnado que investigue en Geogebra cómo representar funciones con restricciones, en vez de darle el código del comando.

 Se puede aplicar como actividad colaborativa, repartiéndose el abecedario entre el alumnado

Tu clase en un clic

Implementa esta microsecuencia en tu aula Moodle (Descarga disponible en gallego o castellano ).

Imaxe

Imaxe