Ágora dixital
Nesta experiencia aprenderemos a resolver o cubo de Rubik, coñecido crebacabezas mecánico, de engranaxes empregando un algoritmo.
Un algoritmo é unha secuencia de pasos precisos empregados para resolver un problema ou realizar unha tarefa. Cando nos enfrontamos a un problema, o algoritmo é unha guía ou procedemento que nos axuda a avanzar pasiño a pasiño cara á solución. Podemos comparalo a unha receita de cociña: seguindo os pasos indicados somos capaces de facer o prato desexado.
De xeito inconsciente, empregas multitude de algoritmos para resolver tarefas ou problemas no teu día a día.

Cesta de materiais
Preme nos puntos interactivos da imaxe.
Mans á obra
- Paso 1
-
- O cubo de Rubik de engranaxes permite menos movementos que o cubo de Rubik tradicional, soamente podemos facer xiros de 180º. Para poñernos mans á obra vamos a revisar como vamos a nomear as filas e columnas do cubo, así como os movementos que vamos a empregar na resolución do mesmo.
Imaxe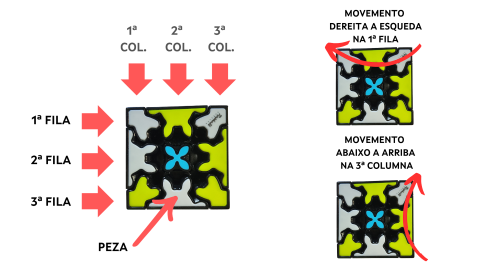
Imaxe propia. Movementos cubo Rubik de engranaxes. - Partimos do cubo de Rubik desfeito, co seguinte algoritmo seremos capaces de resolvelo:
Imaxe
Imaxe propia. Punto de partida do algoritmo. - Paso 2
-
- Colocamos as pezas das esquinas e do centro da mesma cor en todas as caras.
Repetir o movemento:
a) 3ª fila (esquerda a dereita) e 3ª columna (abaixo a arriba), según conveña, para colocar as pezas das esquinas da mesma cor en cada cara.
b) 3ª columna de forma continúa ata que a peza do medio coincida coa cor das pezas das esquinas en cada cara.
Ata: conseguir que as pezas das esquinas e do centro sexan da mesma cor en todas as caras.
Imaxe
Imaxe propia. Paso para a resolución do cubo Rubik de engranaxes. - Colocamos as pezas das esquinas e do centro da mesma cor en todas as caras.
- Paso 3
-
- Aplanamos as pezas das caras.
- Repetir o movemento: 3ª columna de abaixo a arriba
Ata: conseguir aplanar todas as pezas nas caras.
Imaxe
Imaxe propia. Paso para a resolución do cubo Rubik de engranaxes. - Paso 4
-
- Colocamos as pezas intermedias (entre esquinas) da mesma cor que as caras contiguas.
Imaxe
Imaxe propia. Paso para a resolución do cubo Rubik de engranaxes. - Repetir o movemento en cada unha das caras:
a) 3ª columna catro xiros de abaixo a arriba (mover catro veces de abaixo a arriba).
b) 1ª fila dous xiros de dereita a esquerda (mover dúas veces de dereita a esquerda).
Ata: conseguir que as pezas intermedias (pezas entre as esquinas) en cada cara sexan da mesma cor que as caras contiguas.
Imaxe
Imaxe propia. Paso para a resolución do cubo Rubik de engranaxes. - Paso 5
-
- Cuarto, aplanamos as pezas das caras.
- Coloca o cubo de forma que as pezas que non estean planas na fila central estean na cara supeior, mirando cara ti.
- Repetir o movemento: 3ª columna de abaixo a arriba
Ata: conseguir aplanar todas as pezas nas caras.
Imaxe
Imaxe propia. Paso para a resolución do cubo Rubik de engranaxes. - Paso 6
-
- Colocar o cubo de xeito que a fila do medio que ten as cores correctas quede colocada de forma horizontal.
Imaxe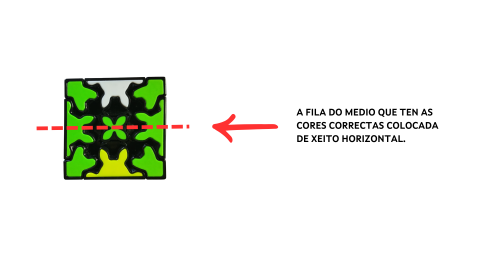
Imaxe propia. Paso para a resolución do cubo Rubik de engranaxes. - Paso 7
-
- Repetir o movemento:
a) 3ª columna dous xiros de abaixo a arriba
b) 1ª fila dous xiros de dereita a esquerda
c) 3ª columna dous xiros de abaixo a arriba
d) 1ª fila dous xiros de dereita a esquerda.
e) 3ª columna dous xiros de abaixo a arriba
f) 1ª fila dous xiros de dereita a esquerda
Ata: resolver o cubo.
Imaxe
Imaxe propia. Paso para a resolución do cubo Rubik de engranaxes. - Repetir o movemento:
Tips docentes
Os tips do profesorado son pequenas axudas para desenvolver a estratexia educativa de forma adecuada.
- Un algoritmo é un conxunto de instrucións precisas e detalladas que seguen unha secuencia lóxica para resolver un problema ou realizar unha tarefa específica. Pódese pensar nun algoritmo como unha receita de cociña, onde se indican os pasos a seguir para preparar un prato determinado. Cada paso debe ser claro e exacto, e debe conducir a un resultado específico.
- Nas matemáticas, os algoritmos son fundamentais porque permiten resolver problemas complexos de maneira sistemática. Por exemplo, os algoritmos de cálculo numérico permiten aos matemáticos resolver ecuacións, calcular derivadas e integrales, e realizar outras operacións matemáticas de maneira eficiente. Tamén se utilizan en áreas como a álxebra e a estatística para desenvolver métodos de solución que poden ser aplicados a unha ampla variedade de problemas. Ata a operación máis básica, sumar dous máis tres, segue un algoritmo.
- Na programación, os algoritmos son a base para desenvolver software. Cando un programador quere que un ordenador realice unha tarefa, debe escribir un algoritmo que describa como se debe realizar esa tarefa. Estes algoritmos son despois traducidos a linguaxes de programación como Python, Java ou C++, que o ordenador pode entender e executar. Por exemplo, un algoritmo de ordenación pode ser usado para organizar unha lista de números de menor a maior, ou un algoritmo de busca pode ser utilizado para encontrar un elemento específico nunha base de datos. Na programación de videoxogos, aplicacións para o móbil, páxinas web e redes sociais, empréganse algoritmos.
- Na intelixencia artificial (IA), os algoritmos son aínda máis cruciais. A intelixencia artificial busca crear máquinas ou programas que poidan realizar tarefas que normalmente requiren intelixencia humana, como aprender de experiencias, recoñecer patróns e tomar decisións. Isto é posible grazas aos algoritmos de aprendizaxe automática, que permiten ás máquinas analizar grandes cantidades de datos, identificar patróns e mellorar o seu rendemento co tempo. As redes neuronais, a regresión lineal e os veciños próximos son exemplos de como se aplican algoritmos na intelixencia artificial para resolver problemas complexos en campos como o recoñecemento de imaxes, a análise de texto e a predición de tendencias.
No apartado de Mans a obra, explicar ao alumnado a historia do cubo de Rubik.
- O cubo de Rubik é unha auténtica xoia da enxeñaría e do entretemento. A súa historia comeza nos anos 70, cando o arquitecto e profesor húngaro Ernő Rubik o inventou inicialmente como unha ferramenta para axudar aos seus alumnos a comprender conceptos de xeometría tridimensional.
Pero aquí ven a anécdota curiosa: Rubik mesmo tivo problemas para resolver o seu propio cubo despois de o montar! Pásalle que a maioría de nós que intentamos resolver o cubo por primeira vez: atopouse cun verdadeiro desafío. Na súa frustración inicial, intentou devolver as pegatinas ás súas posicións correctas, pero finalmente decatouse de que o problema tiña unha solución matemática.
Despois de moitas horas de traballo, Rubik conseguiu resolver o seu propio enigma, dando lugar a un dos xogos de lóxica máis populares do mundo. Desde entón, o cubo de Rubik converteuse nunha sensación global, inspirando a xeracións de xogadores e aficionados a enfrontarse ao desafío de resolver as súas cores mesturadas.
- Existen multitude de variantes do cubo de Rubik como é o de engranaxes que empregamos nesta microsecuencia. Hai cubo de diferentes tamaños e formas, pero todos coinciden en que existe un algoritmo para resolvelos. Na páxina web da tenda de xogos Besa de Culleredo (A Coruña) pódese ver unha mostra da gran variedade de cubos (ligazón: https://www.juegosbesa.com/es/19-cubos-de-rubik)
- Existen competicións de resolver o cubo de Rubik en menos tempo, na actualidade é Mark Park que resolveu o cubo de Rubik 3x3x3 en 3,13 segundos.
A túa clase nun clic
Implementa esta microsecuencia na túa aula Moodle (Descarga dispoñible en galego ou castelán).
|
Imaxe
 |
Imaxe
 |
